本シリーズでは、写真撮影に係わる用語で、本ブログの範囲
でのみ使われたり、一般的では無い専門用語を解説している。
![_c0032138_14500328.jpg]()
用語や、新たに使用している独自用語を、順不同で雑多な
「アラカルト」として紹介しているが、今回は「収差」関連
の内容が多くなっている。
では、早速始めよう。
★大小効果
本ブログ独自用語。
「大型のカメラに小型(薄型)のレンズを装着すると格好良い」
というマニアックな概念。
恐らくだが、銀塩時代の1990年代にCONTAX RTSⅢ(1990年)
にCONTAX Tessar 45mm/F2.8(1982年。1993年に再生産)
のパンケーキ(薄型)レンズを装着したマニアが居て、
雑誌等で紹介され、その様子が「格好良い」と話題に
なったのが元祖だと思われる。
現在、そのものズバリのシステムは組めないが、RTSⅢと
同等のサイズ感を持つCONTAX AX(1996)とTessar 45/2.8
で、その雰囲気を検証してみよう。
![_c0032138_14500358.jpg]()
あった為、1990年代には、MFのCONTAX T45/2.8を除き、
ほぼ絶滅しまっていた。(元々不人気であった事も要因だ)
結局1990年代に「大小効果」を得ようとすると、当時の
現行製品ではCONTAX RTSⅢ or AXにT45/2.8を、組み
合わせるか、又はNIKON F4 or F5に、準パンケーキ型の、
NIKON Ai(E)50/1.8を組み合わせる位しか選択肢が無かった。
この為、1990年代後半には希少な中古薄型レンズを求める
マニア層により、一大「パンケーキブーム」が起こる。
(本シリーズ第9回記事参照)
2000年代、デジタル時代になり、(MF)パンケーキブームは
去ったが、その頃からAFの薄型レンズも少し発売され始め、
2010年代では、一眼レフ用およびミラーレス機用の各種
薄型レンズが色々出ている。(レンズマニアックス第27回、
第28回記事)
ただ、どの組み合わせを取っても、銀塩時代のCONTAX機の
ような極端な「大小効果」は得る事が出来ない。
![_c0032138_14500473.jpg]()
/f2.8 XS(2012年)
まあ、このシステムだと、かなり大きさの差異はあるが、
銀塩時代のCONTAXシステムの感覚には及ば無いであろう。
★ハンドリング(性能)
一般用語、やや独自解釈。
カメラやレンズ、あるいは周辺機器(三脚、ジンバル、電源、
各種計測器、補助部品等)を含む機材全般での、「可搬性」
「取り回し」「振り回し」等の全般を含めて、本ブログでは
「ハンドリング(性能)」と呼ぶ。
一般に、ネガティブな要因で使われるケースが多く、例えば
「重すぎてハンドリング性能が悪い(劣る)」等である。
もう少し詳細には、以下の3つのケースがあると思う。
1)可搬性が悪い。
機材の重量が重い、長さが長い、サイズが大きい等で、
移動や運搬が困難である事。
「機動力が低下する」等と言う場合もある。
2)重量負担が大きい、または巨大で使い難い。
カメラとレンズによる「システム」の総重量が重く、
手持ち撮影が困難であったり、重さ以外にも長さや大きさ
があって使い難い(取り回しが悪い、振り回せない、等)
![_c0032138_14502341.jpg]()
例えばカメラが軽く、レンズが重い、または長いといった
状態において、手持ち撮影の際、本来であれば、カメラと
レンズの重心位置を撮影者は左手で支えるのだが・・
その際、重心位置を持ちにくい(ホールドしにくい)
バランスとなってしまったり、あるいは重心位置を支える
事で、レンズ操作(ズームリング、ピントリング、絞り環、
各種スイッチ類)が、とてもやりにくくなってしまう場合。
又は、望遠ズームレンズや大型マクロレンズ等で、鏡筒の
全長が撮影条件により大きく変化し、その結果として、
重心位置の変動が起こり、システムの全体を支える事や
各種操作(主にレンズ側、稀に本体側)に影響が出てしまう
ケース。(取り回しが悪い、操作性が悪化する等とも言う)
![_c0032138_14502367.jpg]()
「ハンドリング性能が悪化する(している)」等と呼ぶ。
なお、重量級MFレンズに重量級ボディをあてがう事で、
上記3)の重心位置を改善できる場合もあるが、それは大型
の大口径MF単焦点レンズ等での限られたケースである場合が
多く、重心バランスが変動する場合は、ほぼ無効となる。
また、そのケースでは、重すぎて上記1)2)の「可搬性」
とか「振り回し」に強い悪影響が出てくる事が多い。
そのシステムで「手ブレが防げる」等の話も実は根拠が無く、
それよりも重量級システムの手持ち撮影などは疲労を誘発し
長時間の撮影が出来なくなったり、集中力を欠いたりする。
重量級レンズ+重量級ボディの話は、あくまで「銀塩時代の
俗説だ」と思っておくのが良いであろう。現代システムの
場合、実際に試してみれば、大きなメリットは無い事が
すぐに実感できると思う。(高いカメラやレンズを買わせる
為の、宣伝の一種であったのだろう、と解釈している)
また、あえて、重量級レンズに軽量級のボディをあてがう事も
色々試しているが、全長が可変しないレンズの場合等では、
システムの重心位置を意識しておけば何も問題は無く、むしろ
全体重量の軽減の利点が大きい事もわかってきている。
(下写真は、500g台の軽量ボディに、1100g台と、2倍程度も
重い重量級レンズを装着して実用撮影に用いた例)
![_c0032138_14502394.jpg]()
光学原理。
![_c0032138_14502967.jpg]()
カメラ本体の「歪曲(収差)補正」をOFFにして撮影した
ものであり、上部の建物が曲がって写る「樽型歪曲収差」
が出てしまっている。
安価な(ズーム)レンズや、オールド(ズーム)レンズには、
様々な収差が残っていて、それがレンズの描写力を落とす
大きな原因となる。
まあ、必ずしも収差の少ない(良く補正された)レンズの
方が良いレンズだ、とは言い切れないが、それでも気になる
場合はあるだろう。
そんな時、ユーザー側で出来る簡単な対策としては、
「絞って使うと収差は減る」という原理がある。
この事はマニアや中上級ユーザーの間では良く知られている。
では、上記のような「歪曲収差」も絞れば解消するのか?
残念ながら、それは無理だ、絞っても「歪曲収差」は減らない。
具体的に収差の種類毎に対策を挙げておく。
*歪曲収差=画角の3乗に比例して大きくなる。
つまり、広角や超広角になる程、歪曲収差が強くなる。
この収差は描写力そのものには、あまり影響が無く、
カメラ内の補正機能や画像編集ソフトで補正が容易な為、
安価なズームレンズ等の場合は、あまり補正を重要視して
いない設計となっている(参考:レンズ内での絞り部品の
位置を変えるだけでも、歪曲収差の出方に影響がある)
対処方は簡単で、ズームを最広角端から少しだけ望遠側に
廻してやれば良い。それでも歪みが気になる場合とか、
画角的にそう出来ない時は(どうしても広く撮る必要が
ある)上記のカメラ内又はPCでの補正処理を行えば良い。
(注:カメラ内補正は、それに対応しているレンズが必要)
なお、高倍率(高ズーム比)ズームレンズ等では、歪曲
収差の補正を焦点距離(画角)に応じて光学的に行う
仕組みが入っている場合があるが、焦点距離によって、
その補正が効きすぎ、樽型収差の逆の糸巻型歪曲収差が
出てしまうものもある。
*球面収差=有効径の3乗に比例して大きくなる。
すなわち、開放F1.4級等の大口径レンズは小口径レンズに
比べて球面収差が非常に大きくなり、特に絞り開放近くでは
解像感が落ちて甘い描写になる(注:そうならないように
設計すると、複雑で大きく重いレンズとなってしまう、
あるいは非球面レンズを多用すると、コスト高となる)
これについては、単純に絞りを絞り込む事で減少する。
だが、せっかくの大口径レンズだ、絞ると被写界深度が
深くなったり、シャッター速度が低下する等、大口径の
メリットを活かせないので、なかなか厳しい所だ。
なお、開放F1.8級等、F1.4を欲張らないで設計したレンズ
では、開放近くでの球面収差が発生が抑えられていて
比較的良く写るように思えるものが多い(これは他の記事
でも良く書いている「小口径レンズの方が良く写る」だ)
*コマ収差=画角に比例して、および有効径の2乗に
比例して大きくなる。
球面収差とは別の理由による像の滲みの現象。
解像感を弱める他、画面周辺の甘さや、ボケ質へも
影響が出る。
一般に、レンズ設計上では、球面収差とコマ収差は両者を
同時に優先的に補正していると思われる。材質の異なる
凸凹レンズの組み合わせや、両面非球面レンズ等を用いて
これを消す。両者が良く補正された設計を「アプラナート」
と呼ぶ模様だが、専門用語であり一般的な用語では無い。
この収差については、絞り込んで、かつ(ズーミングを)
あまり広角端で使わない事が対策なのだが、単焦点レンズ
の場合、レンズ自体の性能(設計仕様)によりけりの
要素も大きいであろう。
*像面湾曲と非点収差=画角の2乗に比例して、および
有効径に比例して大きくなる。
画面の中心部と周辺部で、ピント位置が変わるのが
「像面湾曲」であり、画面の水平面(サジタル面)と、
垂直面(メリディナル面)でピント位置が変わってしまう
現象が「非点収差」である。
具体的には、画面全体を均一に高い解像力で撮影できなく
なってしまったり、画面周辺の描写が甘く感じてしまう事
(注:これは「球面収差」の影響もある)や、あるいは
ボケ質が悪くなったりする。
両収差は、レンズ設計上では合わせて意識される場合が
殆どで、その評価条件を「ペッツヴァール和」と呼ぶ。
対策としては、絞り込む事で、ある程度解消するが、
完全に無くなる事は無い。
殆どレンズ設計(仕様)に依存する部分であろう。
銀塩の「写ルンです」では、単純なレンズ構成で
ありながら、像面湾曲を減らす為に、なんとフィルムが
湾曲して装填されるようになっていた。デジタル機では
センサーを曲げられないので、この裏技は使えない。
(将来に、柔らかい撮像センサーが開発されれば可能だ)
また、銀塩時代のMINOLTA VFC24/2.8というレンズは、
像面湾曲の発生をコントロール出来るレンズだった。
(注:レアものにつき、未所有)
ところで、「ペッツヴァ(バ)ール」と聞くと、
「ぐるぐるボケ」のレンズを連想するであろう。例えば
「LOMO ペッツヴァール ARTレンズ」や、LENSBABY TWIST、
BURNSIDE等がある。
まあ、その通りであり、それら「ぐるぐるボケ」レンズは、
意図的に像面湾曲と非点収差を強く発生させている設計だ。
よって、それら特殊レンズでは、できるだけ絞りを開けたり
フルサイズ機で画角を広める事で、その「ぐるぐるボケ」
の効果を強める事ができる。(下写真)
![_c0032138_14502956.jpg]()
光の波長(色)毎に、屈折率が異なる事から、色の滲みが
出てしまう現象。特に望遠レンズで大きく、白い被写体等を
撮影した場合に、輪郭線に色が滲んで見えてしまう。
概ねレンズ設計に依存し、色消し(アクロマートや
アポクロマート)構成として、色分散(アッベ数)の異なる
凸凹レンズを組み合わせて設計するが、全波長でこれを
完全に取り除くのは難しい模様だ。
軸上色収差については、絞りを絞り込む事で解消できるが
倍率色収差に関しては、そのまま残ってしまう。
だが、ここもまたレンズ設計次第であろう。
「アポ」等と書いてあるレンズは、これを重点的に補正して
あると思われるが、別にそう書いていなかった場合でも、
あくまで設計次第だ。
なお、紫などの「偽色」が発生する「パープルフリンジ」
も色収差の一種だろうが、カメラの撮像素子の仕様上にも
影響され、この場合は一応絞ってみて、それでもダメならば
カメラ(やレンズ)を変えるしか無いかも知れない。
あと、オールド望遠ズーム等でも色収差は良く発生するが
絞っても消えない「倍率色収差」が残っている場合は、
できるだけ白い被写体(サギ等の野鳥が特に目立つ)を
撮らない、という対策もある。
下写真は、そうしたオールド望遠ズームで、黒い鳥を
撮ったケース。色収差が出ている事は目立た無いのだが、
絞りを絞っていても他の収差も色々残っているレンズの為、
解像感が低く感じてしまうのは否めない。
![_c0032138_14502905.jpg]()
第一の対策なのだが、「それでは解消されない収差もある」
という事だけは覚えておくのが良いであろう。
そして、収差全般については、非常に専門的かつ高度な
内容なので、一般カメラマンが知るべき範疇を超えている。
つまり、あまり勉強してもしかたがない(理解困難)し、
知ったかぶりで、収差について語る事も好ましく無い。
また、歪曲収差の確認など、利用者側で簡単に出来る内容
のみを検証し、「このレンズは優れている(劣っている)」
等の狭い視点での評価(レビュー)を行う事も、他の収差
の事をまるで理解していないようで、好ましく無い。
★MFロック
本ブログ独自用語。
AF測距点数が、1点や3点と少ない銀塩時代のAF機や、
現代機の多点測距機であっても、合焦精度の高い中央の
測距点を使いたいが為に「スポットAF」等に設定している
場合・・
写真の構図によっては、中央(や測距点上)に被写体が
無い場合がある。
こんな時、被写体に、まず中央等のAF測距点でピントを
合わせた後、カメラを振って構図を整えて撮影する。
この技法を一般的に「AFロック」と呼び、この手法は
初級者であっても知っているであろう(・・というか、
多点測距に頼りすぎていて、この技法を知らないとまずい)
![_c0032138_14503549.jpg]()
機や、一眼レフであってもファインダー中央に「スプリット」
等のピント合わせ機構が存在する。この場合でも画面の中央で
しかピント合わせが出来ない/困難で、MFであっても上記の
「AFロック」と、殆ど同じ手順のピント合わせ操作を行う事に
なる。この操作の事を、本ブログでは「MFロック」と呼ぶ場合
があるが、あくまで独自の用語であって世間一般的では無い。
なお、MF機に限らず現代のミラーレス機であっても、MFレンズ
を使ったり、MFモードで撮ったり、又はマウントアダプターを
用いてMF(オールド)レンズを装着した場合、いずれもMFでの
撮影となるが、その精度を高める為、画面(部分)拡大や、
デジタル・スプリットイメージ等の機能を用いる場合がある。
その際、たいていは拡大位置等を変更できるのだが、それが
面倒な場合(注:カメラの操作系仕様に依存するが、拡大の
操作系が練れていないミラーレス機がとても多いという課題)
・・その場合、拡大位置を変えるのが面倒なので、中央部で
ピントを合わせて構図を変える「MFロック」を、この場合にも
使う事がある。
いずれにしても、「MFロック」技法は練習しておくのが良い
事であろう。
★コサイン誤差(セカント誤差)
マニア用語、独自解釈。
上記の「MFロック」や、本来の用語での「AFロック」を
用いて撮影する場合、画面の中央でピントを合わせた距離
を、構図を変えて被写体を画面の端に動かした場合
そこ迄の距離が変わってしまう。(=ピンボケになる)
普通は、その距離差は殆ど無視できるのだが、大口径
レンズでの近距離撮影等で、被写界深度が極端に浅い場合、
その距離差は無視できなくなる。
一般に、この現象を「コサイン誤差」と呼ぶ、勿論、
sin(サイン)、cos(コサイン)、tan(タンジェント)と
学校で習った「三角関数」の「コサイン」の事である。
その距離が変わる状態を、簡単に図示してみよう。
![_c0032138_14503594.gif]()
AFまたはMFで合わせた。ここでカメラを角度θ(シータ)
だけ廻すと、被写体がC位置に変わり、距離ABよりも
距離ACの方が長くなって距離差が出ている事がわかる。
ただし、ここで注意点。
コサイン(cos)の計算だが、三角関数の定義によると、
底辺÷斜辺、つまりAB÷ACとなって、これでは計算の
分母と分子が逆の印象があると思う。
知りたいのは、AC÷ABで距離が伸びた分を計算したいのだ。
(注:画面中央に被写体を置いて、そこでピントを合わせて
から、構図を振って被写体を端に置く事が普通であろう)
つまり、これは、厳密に言えば「コサイン誤差」では無く、
斜辺(AC)を底辺(AB)で割った「正割関数」(または、sec
セカント)を用いるのが正しい。
だから「セカント誤差」と呼ぶのが適正なのだろうが・・
一般に三角関数と言えば「サイン、コサイン、タンジェント」
と習っただろうが、実は三角関数は6種類ある。
sin(正弦),cos(余弦),tan(正接)の他、それぞれの
逆数(分子と分母が反対)の、sec(セカント/正割)、
cosec(コセカント/余割)、cot(コタンジェンド/余接)
の合計6通りが三角関数だ。
だが、世の中のほぼ全員は、高校を卒業したら(あるいは
テストが終わったら)残りの3つの三角関数など、名前すら
完全に忘れてしまっているだろうし・・
業務上で三角関数を用いるエンジニアや学者などでも、
前の3つの他は、まあ使ってもcot(コタンジェント)が
良い所だろうし、それすらも1/tanθという逆数で
簡単に表現できるので、滅多に使わないかもしれない。
同様に、secθ=1/cosθ、cosecθ=1/sinθで、残りも
簡単に求まる。だからエンジニア等であっても、残りの
三角関数の名前はまず使わず、「コサイン分の1」と言えば
理解も出来るし計算を間違う事も無い、だからsec(セカント)
は、まず使われない可哀想な(?)三角関数だ。
なので、冒頭の距離差の問題は、本来は「セカント誤差」と
定義するべきだけど、それだと世の中の誰も理解が不能で
「??」となってしまうから、あえて誤まった「コサイン誤差」
として広めたのではなかろうか?それならば誰でもわかる。
ただ、それでも「コサイン誤差」だけでは「主語」が無くて
意味が不明である。当然、正規の技術用語では無いだろうし、
あまり数学が得意では無いマニア等が用いた(作った)用語
だったのではなかろうか?
ちなみに、「周辺減光」の事を、誰かが「トンネル効果」と
呼んで、それが広まってしまったが、それも、他にノーベル賞
級の重要な技術用語がある為、本ブログでは非推奨の用語だ。
技術分野に詳しくない人(達)が作ったり広めたりしている
技術っぽい用語は、あまり好ましく無い。
で、その名前はともかく、以下では、その距離差がどれくらい
あるのかを計算する。ここはcosθの計算ではなく、本来の
secθ(セカント)による計算だ。
まず角度(θ、シータ)がどれくらいなのか? という
点だが、ここは使用するレンズの焦点距離や撮像センサー
のサイズに依存する、つまり「画角」である。
画角には、「水平」「垂直」「対角線」がある。
実際に距離差が出易いのは、恐らくは水平の構図ではなく
垂直構図であろう、例えば横位置撮影で被写体を端の隅に
置く構図は、ちょっとバランスが悪く感じるので、それを
やったとしても、多分全体幅の2/3迄位か?(下写真)
![_c0032138_14503582.jpg]()
主要被写体を置くケースも出てくる(下写真)
![_c0032138_14504298.jpg]()
カメラを縦に向けただけであり、フィルムやセンサーの
長辺を使っている事には変わり無い。
なので、以下の計算は、あくまで「水平画角」とする。
*水平画角(35mm判フルサイズ機使用の場合)
35mm=約54度
50mm=約40度
85mm=約24度
レンズ焦点距離の選択は3種類考えてみた、これらの焦点距離
のレンズにはF1.4級の大口径版が良く存在しているので
被写界深度も浅い場合があるだろうからだ。
で、この画角数値は横幅いっぱいの場合だ。
「AF/MFロック」は画面中央で行う為、画面の端までの角度は
この半分が最大だ。
では、それらの半分の角度で「secθ」を計算しよう。
*正割(距離)誤差(セカント値、コサイン誤差の逆数)
35mmレンズ:sec27°=約1.12
50mmレンズ:sec20°=約1.06
85mmレンズ:sec12°=約1.02
注:関数電卓等でこの計算をする場合、1/cosθが
簡便であるが、単位がラジアン(rad)であって、
角度(デグリー、deg)では無い事が普通なので
その際は、π(PI)/180を掛けて変換する必要がある。
さて、これは「比率」であるから、距離では無い。
距離にしたい場合は、撮影距離にこの数値を掛けるので
例えば1mの距離に被写体を置いた場合、35mmレンズの
場合は、最大(画面の端)で1.12倍なので、1.12m
つまり最大12cmも距離差が出てしまう事になる。
「結構、距離の誤差が大きいな」と感じる事であろう。
でもまあこれは最大値なので、実際には、画面の完全な
端などに被写体を置く事は集合写真等を除いてまず無い
と思うので、これはあくまで「最大の誤差」である。
そして「被写界深度」がある。後で計算するが、距離の
誤差があっても、それが被写界深度内であればセーフだ。
それと、画角が狭い85mmレンズでは距離差はあまり出ず、
1mの撮影距離であれば1.02m、つまり最大誤差2cmだ。
ただ、85mm/F1.4等の大口径レンズで、最短撮影距離
スレスレの被写体距離1mでは、相当に被写界深度も
浅くなる事が予想される、2cmでもヤバいかも知れない。
やはり、ちゃんと被写界深度を計算してみよう。
いずれのレンズも、F1.4の開放で使う場合だ、なお、
許容錯乱円は、銀塩35mm判での0.03mmを用いる。
(注:デジタル機での許容錯乱円の定義はどうも曖昧だ)
撮影距離は、わかりやすく1mとしておこう。
*F1.4開放、撮影距離1mでの被写界深度
35mmレンズ(F1.4@1m)=約7cm
50mmレンズ(F1.4@1m)=約3.3cm
85mmレンズ(F1.4@1m)=約1.1cm
・・となった。
しかし、やはりダメだ、上記の「コサイン誤差」よりも
被写界深度の方が浅い、これではAF/MFロック状態から
カメラを振るとピンボケになってしまう(汗)
だけど、F1.4の絞り値で1mの撮影距離というのも
かなり極端な撮影条件だ、絞りを少し絞るか、撮影距離を
少し伸ばせば、いずれの場合でも被写界深度は深くなり、
ピンボケのリスクを減らせる。
詳しい計算は冗長になるので省略するが、色々計算して
みた結果、だいたい以下の結論となった。
結論:いずれのレンズを使う場合でも、絞り値をF2以上に
絞るか、撮影距離を2m以上とすれば、コサイン誤差
は被写界深度内に収まる。
良かった・・ 私は、AFロックもMFロックも結構多用する
ので、これが良く無い計算結果であるとやっかいだった。
だが、実際には、現代の一眼レフやミラーレス機では、
「AF多点測距の利用」「MFピーキング機能による画面全体での
ピント確認」「MFシステムでは、スクリーンのマット面での
ピントの確認」などにより、実用上では、あまりこのような
「コサイン誤差」が影響する事は無い。
参考例だが、私は銀塩時代にKONICA HEXAR RF Limited
というレンジファインダー機を一時期使っていた事がある。
その付属レンズは、50mm/F1.2の大口径である。
レンジ機だから、当然、画面中央でしかピント合わせが
出来ない。で、このシステムでの撮影はピンボケを連発して、
腹を立てていた。定価42万円という超高額な機器故に
(注:実際には新品在庫処分で半額で買った)凄い写りを
期待していたのに、ピンボケ頻発は「酷い欠点」に見えて
しまい「このカメラはダメなカメラだ」と、すぐに譲渡して
しまったのだ。
ただ、今から思い起こせば、これは「コサイン誤差」が
結構発生していたのであろう。なにせ大口径のレンズの
特性を活かしたいと思って、最短撮影距離ギリギリでの
撮影とか、被写体を中央に置かない構図等も、当たり前
のようにして撮っていた訳だ。
この問題をちゃんと理解し、技法で回避していたならば、
「ダメなカメラだ」と見限る事も無かったであろう。
結局は「機材の欠点を回避するのは利用者の責任」である。
まあつまり、「コサイン(セカント)誤差」は、
レンジファインダー機で大口径レンズを使った場合、
多くの確率で発生する、という事である。
これは上記の計算結果からも明らかだ。
私は、銀塩時代から、撮影技法が極端に制限される
レンジ機は基本的には好きでは無かったし、まあ何台かは
手元には残してはいるが、デジタル時代の現代においては、
ますます、そうした機材を使う事は無いであろう。
ただまあ、マニア層においては、依然、銀塩レンジ機の
ファン層は多い、そして近年においては、レンジ機用の
F1.2以下級の超大口径レンズも、稀に発売されているし
銀塩時代よりも価格面でも入手がしやすくなって来ている。
もし、現代でなおレンジ機を使うユーザー層において、
そうした大口径レンズを用いる場合、ここで述べた
「コサイン(セカント)誤差」の発生は、かなり意識して
おく必要があるだろう。
これを意識する為には、ここであげた計算を自身の持つ
システムで、一度試しに計算してみる事を推奨する。
ちょっと面倒な計算であるが、一度それをやる事で、
コサイン誤差の原理も、それが起こる条件や限界点等も、
良く理解でき、かつ記憶にも残って覚えるだろうからだ。
★コサイン四乗則
光学原理、技術用語
前述の「コサイン誤差」と、「コサイン四乗則」は
名前が似ているが、原理も内容も全く異なっている。
そして、こちらは正規の技術用語だ。
![_c0032138_14504254.jpg]()
「コサイン四乗則」によるものであり、レンズに入射する
光の角度が光軸に対してθ(シータ)であった際、
その明るさ(輝度)が、(cosθ)^4(注:^は、累乗を
表す記号)の比率で減るという事だ。
特に(超)広角レンズであると、この法則をモロに受けて
しまう、4乗はさすがに強烈であり、
θ=30°で約半分(0.56倍)、θ=45°で1/4(0.25倍)
θ=60°で1/16(0.0625倍)にも光量が落ちて
しまう訳だ。
ただ、周辺減光が、全てコサイン四乗則に起因している訳
では無い。デジタルではセンサーに入射する光が斜めに
なると光量低下が起こる場合もあるし、広義での「口径食」
も、この要因となる(口径食ならば絞り込むと減少するが、
コサイン四乗則は絞り値とは無関係だ)
あるいはレンズフードや厚手のフィルターによる「ケラレ」や、
イメージサークルがセンサーサイズに比べて小さい場合にも、
また、各種のコンバーター系のアタッチメントを使った際にも、
「シフトレンズ」を、必要以上にシフトさせて使った場合にも、
フラッシュが届かない範囲等でも、周辺減光が起こる事がある。
対策としても、できるだけ周辺減光が起こらないように配慮
するというレンズ設計技法もあるだろう。
(例:テレセントリック光学系等)
![_c0032138_14504321.jpg]()
よっては防げない場合もあるだろうし、それに作画表現上
ではむしろ、中央部に置く被写体を強調する効果もあるので
必ずしも欠点であるとは限らない。
TVのCM等の広告分野では、中央部の商品等を強調する為に
周辺減光(ヴィネッテイング)をあえて追加する場合も多々
あるし、トイレンズ効果等のアート表現でも、その手法は
常識である。(ただ、TV CMでのその流行は10年程前であり
皆がそうすると、目新しさが無くなるので減ってしまった)
「コサイン四乗則」は変に有名であるし、レンズの性能上では
「悪い事だ」のように世間では思われ過ぎているかも知れない。
それは光学の原理なのでやむを得ない。重要な事は、ちゃんと
様々な光学原理を理解した上で、それが弱点にならないような
方法論(写真の撮り方)を考えて実践する事だと思う。
---
さて、今回の用語辞典記事はここまでで、
次回補足編の掲載は、また説明が必要な用語がいくつか
溜まった頃とし、そのタイミングは「不定期」としておく。
でのみ使われたり、一般的では無い専門用語を解説している。

用語や、新たに使用している独自用語を、順不同で雑多な
「アラカルト」として紹介しているが、今回は「収差」関連
の内容が多くなっている。
では、早速始めよう。
★大小効果
本ブログ独自用語。
「大型のカメラに小型(薄型)のレンズを装着すると格好良い」
というマニアックな概念。
恐らくだが、銀塩時代の1990年代にCONTAX RTSⅢ(1990年)
にCONTAX Tessar 45mm/F2.8(1982年。1993年に再生産)
のパンケーキ(薄型)レンズを装着したマニアが居て、
雑誌等で紹介され、その様子が「格好良い」と話題に
なったのが元祖だと思われる。
現在、そのものズバリのシステムは組めないが、RTSⅢと
同等のサイズ感を持つCONTAX AX(1996)とTessar 45/2.8
で、その雰囲気を検証してみよう。

あった為、1990年代には、MFのCONTAX T45/2.8を除き、
ほぼ絶滅しまっていた。(元々不人気であった事も要因だ)
結局1990年代に「大小効果」を得ようとすると、当時の
現行製品ではCONTAX RTSⅢ or AXにT45/2.8を、組み
合わせるか、又はNIKON F4 or F5に、準パンケーキ型の、
NIKON Ai(E)50/1.8を組み合わせる位しか選択肢が無かった。
この為、1990年代後半には希少な中古薄型レンズを求める
マニア層により、一大「パンケーキブーム」が起こる。
(本シリーズ第9回記事参照)
2000年代、デジタル時代になり、(MF)パンケーキブームは
去ったが、その頃からAFの薄型レンズも少し発売され始め、
2010年代では、一眼レフ用およびミラーレス機用の各種
薄型レンズが色々出ている。(レンズマニアックス第27回、
第28回記事)
ただ、どの組み合わせを取っても、銀塩時代のCONTAX機の
ような極端な「大小効果」は得る事が出来ない。

/f2.8 XS(2012年)
まあ、このシステムだと、かなり大きさの差異はあるが、
銀塩時代のCONTAXシステムの感覚には及ば無いであろう。
★ハンドリング(性能)
一般用語、やや独自解釈。
カメラやレンズ、あるいは周辺機器(三脚、ジンバル、電源、
各種計測器、補助部品等)を含む機材全般での、「可搬性」
「取り回し」「振り回し」等の全般を含めて、本ブログでは
「ハンドリング(性能)」と呼ぶ。
一般に、ネガティブな要因で使われるケースが多く、例えば
「重すぎてハンドリング性能が悪い(劣る)」等である。
もう少し詳細には、以下の3つのケースがあると思う。
1)可搬性が悪い。
機材の重量が重い、長さが長い、サイズが大きい等で、
移動や運搬が困難である事。
「機動力が低下する」等と言う場合もある。
2)重量負担が大きい、または巨大で使い難い。
カメラとレンズによる「システム」の総重量が重く、
手持ち撮影が困難であったり、重さ以外にも長さや大きさ
があって使い難い(取り回しが悪い、振り回せない、等)

例えばカメラが軽く、レンズが重い、または長いといった
状態において、手持ち撮影の際、本来であれば、カメラと
レンズの重心位置を撮影者は左手で支えるのだが・・
その際、重心位置を持ちにくい(ホールドしにくい)
バランスとなってしまったり、あるいは重心位置を支える
事で、レンズ操作(ズームリング、ピントリング、絞り環、
各種スイッチ類)が、とてもやりにくくなってしまう場合。
又は、望遠ズームレンズや大型マクロレンズ等で、鏡筒の
全長が撮影条件により大きく変化し、その結果として、
重心位置の変動が起こり、システムの全体を支える事や
各種操作(主にレンズ側、稀に本体側)に影響が出てしまう
ケース。(取り回しが悪い、操作性が悪化する等とも言う)

「ハンドリング性能が悪化する(している)」等と呼ぶ。
なお、重量級MFレンズに重量級ボディをあてがう事で、
上記3)の重心位置を改善できる場合もあるが、それは大型
の大口径MF単焦点レンズ等での限られたケースである場合が
多く、重心バランスが変動する場合は、ほぼ無効となる。
また、そのケースでは、重すぎて上記1)2)の「可搬性」
とか「振り回し」に強い悪影響が出てくる事が多い。
そのシステムで「手ブレが防げる」等の話も実は根拠が無く、
それよりも重量級システムの手持ち撮影などは疲労を誘発し
長時間の撮影が出来なくなったり、集中力を欠いたりする。
重量級レンズ+重量級ボディの話は、あくまで「銀塩時代の
俗説だ」と思っておくのが良いであろう。現代システムの
場合、実際に試してみれば、大きなメリットは無い事が
すぐに実感できると思う。(高いカメラやレンズを買わせる
為の、宣伝の一種であったのだろう、と解釈している)
また、あえて、重量級レンズに軽量級のボディをあてがう事も
色々試しているが、全長が可変しないレンズの場合等では、
システムの重心位置を意識しておけば何も問題は無く、むしろ
全体重量の軽減の利点が大きい事もわかってきている。
(下写真は、500g台の軽量ボディに、1100g台と、2倍程度も
重い重量級レンズを装着して実用撮影に用いた例)

光学原理。

カメラ本体の「歪曲(収差)補正」をOFFにして撮影した
ものであり、上部の建物が曲がって写る「樽型歪曲収差」
が出てしまっている。
安価な(ズーム)レンズや、オールド(ズーム)レンズには、
様々な収差が残っていて、それがレンズの描写力を落とす
大きな原因となる。
まあ、必ずしも収差の少ない(良く補正された)レンズの
方が良いレンズだ、とは言い切れないが、それでも気になる
場合はあるだろう。
そんな時、ユーザー側で出来る簡単な対策としては、
「絞って使うと収差は減る」という原理がある。
この事はマニアや中上級ユーザーの間では良く知られている。
では、上記のような「歪曲収差」も絞れば解消するのか?
残念ながら、それは無理だ、絞っても「歪曲収差」は減らない。
具体的に収差の種類毎に対策を挙げておく。
*歪曲収差=画角の3乗に比例して大きくなる。
つまり、広角や超広角になる程、歪曲収差が強くなる。
この収差は描写力そのものには、あまり影響が無く、
カメラ内の補正機能や画像編集ソフトで補正が容易な為、
安価なズームレンズ等の場合は、あまり補正を重要視して
いない設計となっている(参考:レンズ内での絞り部品の
位置を変えるだけでも、歪曲収差の出方に影響がある)
対処方は簡単で、ズームを最広角端から少しだけ望遠側に
廻してやれば良い。それでも歪みが気になる場合とか、
画角的にそう出来ない時は(どうしても広く撮る必要が
ある)上記のカメラ内又はPCでの補正処理を行えば良い。
(注:カメラ内補正は、それに対応しているレンズが必要)
なお、高倍率(高ズーム比)ズームレンズ等では、歪曲
収差の補正を焦点距離(画角)に応じて光学的に行う
仕組みが入っている場合があるが、焦点距離によって、
その補正が効きすぎ、樽型収差の逆の糸巻型歪曲収差が
出てしまうものもある。
*球面収差=有効径の3乗に比例して大きくなる。
すなわち、開放F1.4級等の大口径レンズは小口径レンズに
比べて球面収差が非常に大きくなり、特に絞り開放近くでは
解像感が落ちて甘い描写になる(注:そうならないように
設計すると、複雑で大きく重いレンズとなってしまう、
あるいは非球面レンズを多用すると、コスト高となる)
これについては、単純に絞りを絞り込む事で減少する。
だが、せっかくの大口径レンズだ、絞ると被写界深度が
深くなったり、シャッター速度が低下する等、大口径の
メリットを活かせないので、なかなか厳しい所だ。
なお、開放F1.8級等、F1.4を欲張らないで設計したレンズ
では、開放近くでの球面収差が発生が抑えられていて
比較的良く写るように思えるものが多い(これは他の記事
でも良く書いている「小口径レンズの方が良く写る」だ)
*コマ収差=画角に比例して、および有効径の2乗に
比例して大きくなる。
球面収差とは別の理由による像の滲みの現象。
解像感を弱める他、画面周辺の甘さや、ボケ質へも
影響が出る。
一般に、レンズ設計上では、球面収差とコマ収差は両者を
同時に優先的に補正していると思われる。材質の異なる
凸凹レンズの組み合わせや、両面非球面レンズ等を用いて
これを消す。両者が良く補正された設計を「アプラナート」
と呼ぶ模様だが、専門用語であり一般的な用語では無い。
この収差については、絞り込んで、かつ(ズーミングを)
あまり広角端で使わない事が対策なのだが、単焦点レンズ
の場合、レンズ自体の性能(設計仕様)によりけりの
要素も大きいであろう。
*像面湾曲と非点収差=画角の2乗に比例して、および
有効径に比例して大きくなる。
画面の中心部と周辺部で、ピント位置が変わるのが
「像面湾曲」であり、画面の水平面(サジタル面)と、
垂直面(メリディナル面)でピント位置が変わってしまう
現象が「非点収差」である。
具体的には、画面全体を均一に高い解像力で撮影できなく
なってしまったり、画面周辺の描写が甘く感じてしまう事
(注:これは「球面収差」の影響もある)や、あるいは
ボケ質が悪くなったりする。
両収差は、レンズ設計上では合わせて意識される場合が
殆どで、その評価条件を「ペッツヴァール和」と呼ぶ。
対策としては、絞り込む事で、ある程度解消するが、
完全に無くなる事は無い。
殆どレンズ設計(仕様)に依存する部分であろう。
銀塩の「写ルンです」では、単純なレンズ構成で
ありながら、像面湾曲を減らす為に、なんとフィルムが
湾曲して装填されるようになっていた。デジタル機では
センサーを曲げられないので、この裏技は使えない。
(将来に、柔らかい撮像センサーが開発されれば可能だ)
また、銀塩時代のMINOLTA VFC24/2.8というレンズは、
像面湾曲の発生をコントロール出来るレンズだった。
(注:レアものにつき、未所有)
ところで、「ペッツヴァ(バ)ール」と聞くと、
「ぐるぐるボケ」のレンズを連想するであろう。例えば
「LOMO ペッツヴァール ARTレンズ」や、LENSBABY TWIST、
BURNSIDE等がある。
まあ、その通りであり、それら「ぐるぐるボケ」レンズは、
意図的に像面湾曲と非点収差を強く発生させている設計だ。
よって、それら特殊レンズでは、できるだけ絞りを開けたり
フルサイズ機で画角を広める事で、その「ぐるぐるボケ」
の効果を強める事ができる。(下写真)

光の波長(色)毎に、屈折率が異なる事から、色の滲みが
出てしまう現象。特に望遠レンズで大きく、白い被写体等を
撮影した場合に、輪郭線に色が滲んで見えてしまう。
概ねレンズ設計に依存し、色消し(アクロマートや
アポクロマート)構成として、色分散(アッベ数)の異なる
凸凹レンズを組み合わせて設計するが、全波長でこれを
完全に取り除くのは難しい模様だ。
軸上色収差については、絞りを絞り込む事で解消できるが
倍率色収差に関しては、そのまま残ってしまう。
だが、ここもまたレンズ設計次第であろう。
「アポ」等と書いてあるレンズは、これを重点的に補正して
あると思われるが、別にそう書いていなかった場合でも、
あくまで設計次第だ。
なお、紫などの「偽色」が発生する「パープルフリンジ」
も色収差の一種だろうが、カメラの撮像素子の仕様上にも
影響され、この場合は一応絞ってみて、それでもダメならば
カメラ(やレンズ)を変えるしか無いかも知れない。
あと、オールド望遠ズーム等でも色収差は良く発生するが
絞っても消えない「倍率色収差」が残っている場合は、
できるだけ白い被写体(サギ等の野鳥が特に目立つ)を
撮らない、という対策もある。
下写真は、そうしたオールド望遠ズームで、黒い鳥を
撮ったケース。色収差が出ている事は目立た無いのだが、
絞りを絞っていても他の収差も色々残っているレンズの為、
解像感が低く感じてしまうのは否めない。

第一の対策なのだが、「それでは解消されない収差もある」
という事だけは覚えておくのが良いであろう。
そして、収差全般については、非常に専門的かつ高度な
内容なので、一般カメラマンが知るべき範疇を超えている。
つまり、あまり勉強してもしかたがない(理解困難)し、
知ったかぶりで、収差について語る事も好ましく無い。
また、歪曲収差の確認など、利用者側で簡単に出来る内容
のみを検証し、「このレンズは優れている(劣っている)」
等の狭い視点での評価(レビュー)を行う事も、他の収差
の事をまるで理解していないようで、好ましく無い。
★MFロック
本ブログ独自用語。
AF測距点数が、1点や3点と少ない銀塩時代のAF機や、
現代機の多点測距機であっても、合焦精度の高い中央の
測距点を使いたいが為に「スポットAF」等に設定している
場合・・
写真の構図によっては、中央(や測距点上)に被写体が
無い場合がある。
こんな時、被写体に、まず中央等のAF測距点でピントを
合わせた後、カメラを振って構図を整えて撮影する。
この技法を一般的に「AFロック」と呼び、この手法は
初級者であっても知っているであろう(・・というか、
多点測距に頼りすぎていて、この技法を知らないとまずい)

機や、一眼レフであってもファインダー中央に「スプリット」
等のピント合わせ機構が存在する。この場合でも画面の中央で
しかピント合わせが出来ない/困難で、MFであっても上記の
「AFロック」と、殆ど同じ手順のピント合わせ操作を行う事に
なる。この操作の事を、本ブログでは「MFロック」と呼ぶ場合
があるが、あくまで独自の用語であって世間一般的では無い。
なお、MF機に限らず現代のミラーレス機であっても、MFレンズ
を使ったり、MFモードで撮ったり、又はマウントアダプターを
用いてMF(オールド)レンズを装着した場合、いずれもMFでの
撮影となるが、その精度を高める為、画面(部分)拡大や、
デジタル・スプリットイメージ等の機能を用いる場合がある。
その際、たいていは拡大位置等を変更できるのだが、それが
面倒な場合(注:カメラの操作系仕様に依存するが、拡大の
操作系が練れていないミラーレス機がとても多いという課題)
・・その場合、拡大位置を変えるのが面倒なので、中央部で
ピントを合わせて構図を変える「MFロック」を、この場合にも
使う事がある。
いずれにしても、「MFロック」技法は練習しておくのが良い
事であろう。
★コサイン誤差(セカント誤差)
マニア用語、独自解釈。
上記の「MFロック」や、本来の用語での「AFロック」を
用いて撮影する場合、画面の中央でピントを合わせた距離
を、構図を変えて被写体を画面の端に動かした場合
そこ迄の距離が変わってしまう。(=ピンボケになる)
普通は、その距離差は殆ど無視できるのだが、大口径
レンズでの近距離撮影等で、被写界深度が極端に浅い場合、
その距離差は無視できなくなる。
一般に、この現象を「コサイン誤差」と呼ぶ、勿論、
sin(サイン)、cos(コサイン)、tan(タンジェント)と
学校で習った「三角関数」の「コサイン」の事である。
その距離が変わる状態を、簡単に図示してみよう。
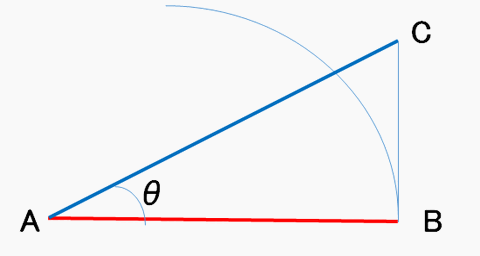
AFまたはMFで合わせた。ここでカメラを角度θ(シータ)
だけ廻すと、被写体がC位置に変わり、距離ABよりも
距離ACの方が長くなって距離差が出ている事がわかる。
ただし、ここで注意点。
コサイン(cos)の計算だが、三角関数の定義によると、
底辺÷斜辺、つまりAB÷ACとなって、これでは計算の
分母と分子が逆の印象があると思う。
知りたいのは、AC÷ABで距離が伸びた分を計算したいのだ。
(注:画面中央に被写体を置いて、そこでピントを合わせて
から、構図を振って被写体を端に置く事が普通であろう)
つまり、これは、厳密に言えば「コサイン誤差」では無く、
斜辺(AC)を底辺(AB)で割った「正割関数」(または、sec
セカント)を用いるのが正しい。
だから「セカント誤差」と呼ぶのが適正なのだろうが・・
一般に三角関数と言えば「サイン、コサイン、タンジェント」
と習っただろうが、実は三角関数は6種類ある。
sin(正弦),cos(余弦),tan(正接)の他、それぞれの
逆数(分子と分母が反対)の、sec(セカント/正割)、
cosec(コセカント/余割)、cot(コタンジェンド/余接)
の合計6通りが三角関数だ。
だが、世の中のほぼ全員は、高校を卒業したら(あるいは
テストが終わったら)残りの3つの三角関数など、名前すら
完全に忘れてしまっているだろうし・・
業務上で三角関数を用いるエンジニアや学者などでも、
前の3つの他は、まあ使ってもcot(コタンジェント)が
良い所だろうし、それすらも1/tanθという逆数で
簡単に表現できるので、滅多に使わないかもしれない。
同様に、secθ=1/cosθ、cosecθ=1/sinθで、残りも
簡単に求まる。だからエンジニア等であっても、残りの
三角関数の名前はまず使わず、「コサイン分の1」と言えば
理解も出来るし計算を間違う事も無い、だからsec(セカント)
は、まず使われない可哀想な(?)三角関数だ。
なので、冒頭の距離差の問題は、本来は「セカント誤差」と
定義するべきだけど、それだと世の中の誰も理解が不能で
「??」となってしまうから、あえて誤まった「コサイン誤差」
として広めたのではなかろうか?それならば誰でもわかる。
ただ、それでも「コサイン誤差」だけでは「主語」が無くて
意味が不明である。当然、正規の技術用語では無いだろうし、
あまり数学が得意では無いマニア等が用いた(作った)用語
だったのではなかろうか?
ちなみに、「周辺減光」の事を、誰かが「トンネル効果」と
呼んで、それが広まってしまったが、それも、他にノーベル賞
級の重要な技術用語がある為、本ブログでは非推奨の用語だ。
技術分野に詳しくない人(達)が作ったり広めたりしている
技術っぽい用語は、あまり好ましく無い。
で、その名前はともかく、以下では、その距離差がどれくらい
あるのかを計算する。ここはcosθの計算ではなく、本来の
secθ(セカント)による計算だ。
まず角度(θ、シータ)がどれくらいなのか? という
点だが、ここは使用するレンズの焦点距離や撮像センサー
のサイズに依存する、つまり「画角」である。
画角には、「水平」「垂直」「対角線」がある。
実際に距離差が出易いのは、恐らくは水平の構図ではなく
垂直構図であろう、例えば横位置撮影で被写体を端の隅に
置く構図は、ちょっとバランスが悪く感じるので、それを
やったとしても、多分全体幅の2/3迄位か?(下写真)

主要被写体を置くケースも出てくる(下写真)

カメラを縦に向けただけであり、フィルムやセンサーの
長辺を使っている事には変わり無い。
なので、以下の計算は、あくまで「水平画角」とする。
*水平画角(35mm判フルサイズ機使用の場合)
35mm=約54度
50mm=約40度
85mm=約24度
レンズ焦点距離の選択は3種類考えてみた、これらの焦点距離
のレンズにはF1.4級の大口径版が良く存在しているので
被写界深度も浅い場合があるだろうからだ。
で、この画角数値は横幅いっぱいの場合だ。
「AF/MFロック」は画面中央で行う為、画面の端までの角度は
この半分が最大だ。
では、それらの半分の角度で「secθ」を計算しよう。
*正割(距離)誤差(セカント値、コサイン誤差の逆数)
35mmレンズ:sec27°=約1.12
50mmレンズ:sec20°=約1.06
85mmレンズ:sec12°=約1.02
注:関数電卓等でこの計算をする場合、1/cosθが
簡便であるが、単位がラジアン(rad)であって、
角度(デグリー、deg)では無い事が普通なので
その際は、π(PI)/180を掛けて変換する必要がある。
さて、これは「比率」であるから、距離では無い。
距離にしたい場合は、撮影距離にこの数値を掛けるので
例えば1mの距離に被写体を置いた場合、35mmレンズの
場合は、最大(画面の端)で1.12倍なので、1.12m
つまり最大12cmも距離差が出てしまう事になる。
「結構、距離の誤差が大きいな」と感じる事であろう。
でもまあこれは最大値なので、実際には、画面の完全な
端などに被写体を置く事は集合写真等を除いてまず無い
と思うので、これはあくまで「最大の誤差」である。
そして「被写界深度」がある。後で計算するが、距離の
誤差があっても、それが被写界深度内であればセーフだ。
それと、画角が狭い85mmレンズでは距離差はあまり出ず、
1mの撮影距離であれば1.02m、つまり最大誤差2cmだ。
ただ、85mm/F1.4等の大口径レンズで、最短撮影距離
スレスレの被写体距離1mでは、相当に被写界深度も
浅くなる事が予想される、2cmでもヤバいかも知れない。
やはり、ちゃんと被写界深度を計算してみよう。
いずれのレンズも、F1.4の開放で使う場合だ、なお、
許容錯乱円は、銀塩35mm判での0.03mmを用いる。
(注:デジタル機での許容錯乱円の定義はどうも曖昧だ)
撮影距離は、わかりやすく1mとしておこう。
*F1.4開放、撮影距離1mでの被写界深度
35mmレンズ(F1.4@1m)=約7cm
50mmレンズ(F1.4@1m)=約3.3cm
85mmレンズ(F1.4@1m)=約1.1cm
・・となった。
しかし、やはりダメだ、上記の「コサイン誤差」よりも
被写界深度の方が浅い、これではAF/MFロック状態から
カメラを振るとピンボケになってしまう(汗)
だけど、F1.4の絞り値で1mの撮影距離というのも
かなり極端な撮影条件だ、絞りを少し絞るか、撮影距離を
少し伸ばせば、いずれの場合でも被写界深度は深くなり、
ピンボケのリスクを減らせる。
詳しい計算は冗長になるので省略するが、色々計算して
みた結果、だいたい以下の結論となった。
結論:いずれのレンズを使う場合でも、絞り値をF2以上に
絞るか、撮影距離を2m以上とすれば、コサイン誤差
は被写界深度内に収まる。
良かった・・ 私は、AFロックもMFロックも結構多用する
ので、これが良く無い計算結果であるとやっかいだった。
だが、実際には、現代の一眼レフやミラーレス機では、
「AF多点測距の利用」「MFピーキング機能による画面全体での
ピント確認」「MFシステムでは、スクリーンのマット面での
ピントの確認」などにより、実用上では、あまりこのような
「コサイン誤差」が影響する事は無い。
参考例だが、私は銀塩時代にKONICA HEXAR RF Limited
というレンジファインダー機を一時期使っていた事がある。
その付属レンズは、50mm/F1.2の大口径である。
レンジ機だから、当然、画面中央でしかピント合わせが
出来ない。で、このシステムでの撮影はピンボケを連発して、
腹を立てていた。定価42万円という超高額な機器故に
(注:実際には新品在庫処分で半額で買った)凄い写りを
期待していたのに、ピンボケ頻発は「酷い欠点」に見えて
しまい「このカメラはダメなカメラだ」と、すぐに譲渡して
しまったのだ。
ただ、今から思い起こせば、これは「コサイン誤差」が
結構発生していたのであろう。なにせ大口径のレンズの
特性を活かしたいと思って、最短撮影距離ギリギリでの
撮影とか、被写体を中央に置かない構図等も、当たり前
のようにして撮っていた訳だ。
この問題をちゃんと理解し、技法で回避していたならば、
「ダメなカメラだ」と見限る事も無かったであろう。
結局は「機材の欠点を回避するのは利用者の責任」である。
まあつまり、「コサイン(セカント)誤差」は、
レンジファインダー機で大口径レンズを使った場合、
多くの確率で発生する、という事である。
これは上記の計算結果からも明らかだ。
私は、銀塩時代から、撮影技法が極端に制限される
レンジ機は基本的には好きでは無かったし、まあ何台かは
手元には残してはいるが、デジタル時代の現代においては、
ますます、そうした機材を使う事は無いであろう。
ただまあ、マニア層においては、依然、銀塩レンジ機の
ファン層は多い、そして近年においては、レンジ機用の
F1.2以下級の超大口径レンズも、稀に発売されているし
銀塩時代よりも価格面でも入手がしやすくなって来ている。
もし、現代でなおレンジ機を使うユーザー層において、
そうした大口径レンズを用いる場合、ここで述べた
「コサイン(セカント)誤差」の発生は、かなり意識して
おく必要があるだろう。
これを意識する為には、ここであげた計算を自身の持つ
システムで、一度試しに計算してみる事を推奨する。
ちょっと面倒な計算であるが、一度それをやる事で、
コサイン誤差の原理も、それが起こる条件や限界点等も、
良く理解でき、かつ記憶にも残って覚えるだろうからだ。
★コサイン四乗則
光学原理、技術用語
前述の「コサイン誤差」と、「コサイン四乗則」は
名前が似ているが、原理も内容も全く異なっている。
そして、こちらは正規の技術用語だ。

「コサイン四乗則」によるものであり、レンズに入射する
光の角度が光軸に対してθ(シータ)であった際、
その明るさ(輝度)が、(cosθ)^4(注:^は、累乗を
表す記号)の比率で減るという事だ。
特に(超)広角レンズであると、この法則をモロに受けて
しまう、4乗はさすがに強烈であり、
θ=30°で約半分(0.56倍)、θ=45°で1/4(0.25倍)
θ=60°で1/16(0.0625倍)にも光量が落ちて
しまう訳だ。
ただ、周辺減光が、全てコサイン四乗則に起因している訳
では無い。デジタルではセンサーに入射する光が斜めに
なると光量低下が起こる場合もあるし、広義での「口径食」
も、この要因となる(口径食ならば絞り込むと減少するが、
コサイン四乗則は絞り値とは無関係だ)
あるいはレンズフードや厚手のフィルターによる「ケラレ」や、
イメージサークルがセンサーサイズに比べて小さい場合にも、
また、各種のコンバーター系のアタッチメントを使った際にも、
「シフトレンズ」を、必要以上にシフトさせて使った場合にも、
フラッシュが届かない範囲等でも、周辺減光が起こる事がある。
対策としても、できるだけ周辺減光が起こらないように配慮
するというレンズ設計技法もあるだろう。
(例:テレセントリック光学系等)

よっては防げない場合もあるだろうし、それに作画表現上
ではむしろ、中央部に置く被写体を強調する効果もあるので
必ずしも欠点であるとは限らない。
TVのCM等の広告分野では、中央部の商品等を強調する為に
周辺減光(ヴィネッテイング)をあえて追加する場合も多々
あるし、トイレンズ効果等のアート表現でも、その手法は
常識である。(ただ、TV CMでのその流行は10年程前であり
皆がそうすると、目新しさが無くなるので減ってしまった)
「コサイン四乗則」は変に有名であるし、レンズの性能上では
「悪い事だ」のように世間では思われ過ぎているかも知れない。
それは光学の原理なのでやむを得ない。重要な事は、ちゃんと
様々な光学原理を理解した上で、それが弱点にならないような
方法論(写真の撮り方)を考えて実践する事だと思う。
---
さて、今回の用語辞典記事はここまでで、
次回補足編の掲載は、また説明が必要な用語がいくつか
溜まった頃とし、そのタイミングは「不定期」としておく。